走行計算 for ワールドドローム　その２
基礎的なシミュレーションシステムを確立
最適ギア比の推測
08 Apr 2000

---

　走行計算用エクセルファイルを公開しました。このページの一番下をご覧ください。　

　注意：本ページの記述は多くの仮定を含んだ、あくまでも基礎的なものである点をご留意ください。

　ドローム開催まであと２ヶ月、準備も大詰めです。
と、いうわけでいよいよ走行シミュレーション本体の検討をはじめました。なんか違ってるような気がしますが、ま、いいか。

（１）シミュレーションシステム確立

　ドロームでは、通常のサーキットと異なりコーナリング性能よりも最高速度が重要となります。「最高速度」というのは、モーターの発生する加速力と、空気抵抗、走行抵抗などの減速力がつりあっている状態です。

　基本的にはこれまでに検討してきたラジコンの走行シミュレーションシステムをそのまま適用可能だと思われますが、ドロームでは傾斜のついたバンクコースですので、そのあたりの要因を加味する必要があります。
　バンクでは車体横方向に複雑な力が働きます（バンクコースでのコーナリングフォース推測参照）。重力の一部はコーナリングフォースに使われ、コーナー旋回の遠心力の一部は車体を上から押さえつける（以下「縦G」）力として働きます。



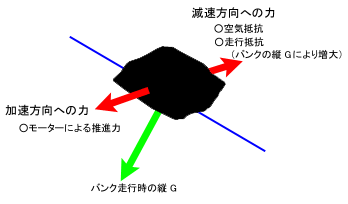　この「縦G」がバンク走行を考える時に重要となります。車両を減速させようとする力として、主に「空気抵抗」と「走行抵抗」が考えられます。このうち、走行抵抗は主にタイヤ接地面の摩擦力に起因する抵抗力なのですが、これがシャシー垂直方向の力、つまり縦Gに比例して強くなってしまうのです。つまり、縦Gが大きくなるバンクコーナー部分では減速方向への力が強くなる、ということになり、直線部分の最高速度から徐々に減速することになります。

　CSC250ｍピスト走行時には「バンク角のついた直線部分」も存在します。この非コーナリング時には遠心力がはたらきませんから垂直方向には重力（１G)しか作用しません。さらにこの場合にはバンク角があるので、シャシーに対して垂直にはたらく力成分は1Gより小さくなります。このため走行抵抗は小さくなる可能性もありますが、水平方向に、バンクの底に落ちようとする力に対抗するためにいくらかの抵抗が生じていることを考え合わせますと、このあたりは厳密に考えるのが困難なので、「直線部分での走行抵抗の合計は1G下での抵抗と同じ大きさである」と仮定しています。


　以上をふまえて具体的な計算を行います。単位時間あたり（例えば０．１秒ごとに）で各要素値を計算し、それを反復することで走行プロフィールを求めます。

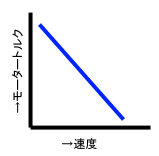１．区間初速からモーター回転数およびトルクを求めます。モーターの回転数とトルクは負に比例しますから、回転数が上がるにつれトルクは下がっていきます。一方空気抵抗を含む減速力は増大していきますので。両者がつりあう点で速度一定（最高速）となります。
２．累積走行距離からコース中での現在位置およびバンク角を求めます。コースの幾何は下図のように推測、仮定しています。（コース内側ラインを走行）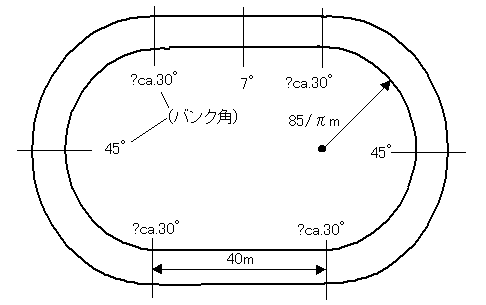

３．減速方向に働く力を計算します。空気抵抗は速度＾２に比例する力で、走行抵抗はシャシー垂直方向に働く力に比例します。

４．モーターのトルクと減速力の差を計算し、正の値であれば加速、負であれば減速します。区間平均速度から区間走行距離を算出します。

　パラメータは過去のデータをもとに以下の値を使用しました。（かわにしはスーパートラッククラスへの参加を予定しています）

車重	1.3kg	PIC積んで重め^^;)を予想
駆動輪直径	62mm	BSR
ギア比	1.8	適宜変えて計算してみる
転がり抵抗係数	0.05	実測値より類推
空気抵抗係数	0.45	ツーリングハコボディ実測値を参考に
前面投影面積	0.02m^2	同上
回転部分相当重量	0.13kg	車重の10％

モーターパワーは以下の実測値を参考にしました。

	最高回転数	静止時トルク
23T	28000rpm	1805g-cm	カワダVstock
27T	20100rpm	1770g-cm	ヨコモProstockII

まず、2000年のデータと比較するため23Tでシミュレーションしてみました。

　各ステップごとの計算はエクセルで行いました。（一部抜粋）

経過時間(s)	累積走行距離(m)	バンク角（°）	縦G	初速m/s	モーター回転数rpm	モータートルクkg-cm	推進力kg	ころがり抵抗kg	空気抵抗kg	加速推進力kg	区間加速度m/s^2	区間終速m/s
7.30	172.55	39.72	2.311	25.29	14031	0.900	0.497	0.150	0.360	-0.013	-0.091	25.283
7.40	175.08	40.62	2.329	25.28	14026	0.901	0.497	0.151	0.360	-0.014	-0.096	25.274
7.50	177.60	41.51	2.345	25.27	14021	0.901	0.497	0.152	0.359	-0.015	-0.101	25.264
7.60	180.13	42.40	2.362	25.26	14015	0.902	0.497	0.154	0.359	-0.015	-0.104	25.253

その結果は・・・、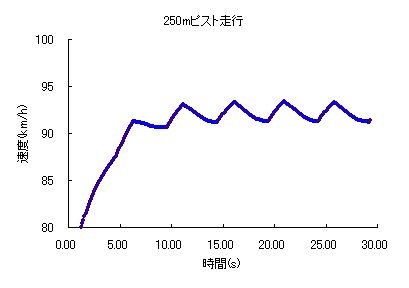
　10秒まで加速し、その後は定常状態にはいります。のこぎり型のグラフは直線部分の加速とコーナー部分での減速を示しています。２周期分でバンク一周、ということになります。

　この計算の結果、

周回平均スピード	92.2km/h
ラップタイム	9.76s

となりました。2000年ドローム予選トップのラップが9.62sですから、まずまずの結果だといえます。

次に、ギア比を変えて計算してみました。

ギア比	ラップ(s)
1.6	9.80
1.7	9.78
1.8	9.76
1.9	9.78
2.0	9.82

かなり微妙な比較ですが、一応最適なギア比は1.8前後であると言えます。ドローム2000ではピニオン48/スパー88、ギア比で1.83の組み合わせが最も使われていたようですから、これも妥当であるといえます。

（２）ドローム2001のシミュレーション

　このシステムを使い、いろいろとパラメータを変えてラップタイムを計算してみましょう。

１．27Tモーターでの最適ギア比
　今年のドロームは27Tの支給モーターの使用が義務付けられています。この特製モーターのスペックはまだわかっていないのですが、以前測定したヨコモの２７Tの測定値を参考にしました。その結果は

ギア比	ラップ(s)
1.2	11.24
1.3	11.14
1.4	11.11
1.5	11.11
1.6	11.14
1.7	11.22
1.8	11.30

・・・これはまた微妙ですが、これによると最適ギア比は1.4-1.5ということになるのかな？・・・なんか低すぎですね・・？
78Tスパー使っても、ピニオン52〜55T！！ううむ・・。一応準備だけはしときましょうか･･。公式モーターの実測も必要ですね．

２．他のパラメータを変えた時の影響

	ラップタイム（s）
標準パラメータ	11.11
車重+10％	+0.10
駆動効率5％ダウン	+0.22
転がり抵抗5％アップ	+0.06
ボディ前面面積5％アップ	+0.14
モーター最高回転数5%up	-0.06

　ぱっとみたかんじでは、
○駆動効率には気を使う必要がある
○車重はそれほど影響しない→PICをガンガン載せられる＾＾）
・・・といったところでしょうか。

　とりあえず今回はここまで。

　ダウンロード後、解凍してください。
　「パラメータ＆計算結果」シートの、パラメータ入力欄（車体重量〜コーナリング半径まで）の数値を入力すると右側のグラフとラップタイムの値に反映されます。計算式自体は「走行計算」シートに記述されています。

---